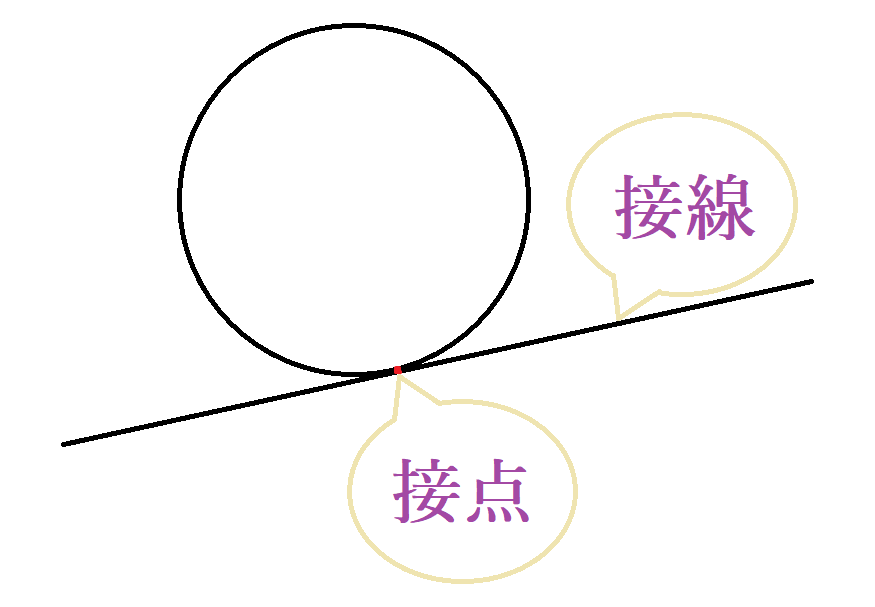
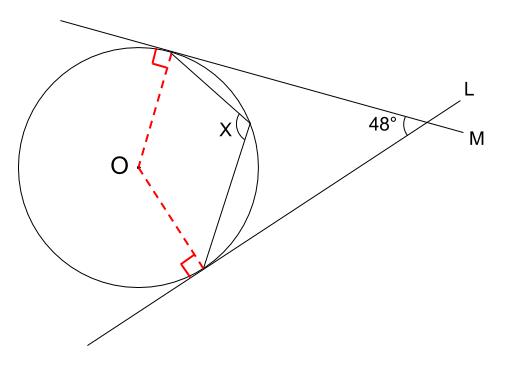
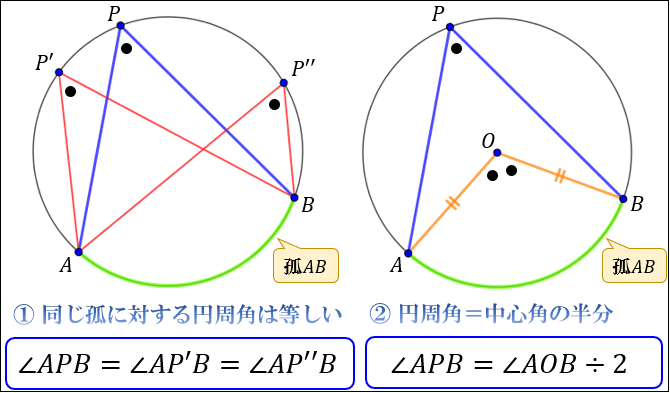
今回は、こんな質問をいただきました↓点(4, 6)を通り、円 (x -1)2 (y - 1)2 = 9 に接する直線の方程式は?この問題、直接書いてないですが、円の接線を求める問題です。円の接線を求める問題には、与えられる条件によって、円 接線 角度 中学 円 接線 角度 中学円の接線によってできる角度の問題を解いてみましょう。はじめに、基礎知識を確認します。 円に接線を引くと、接点で半径と垂直に交わる。 問題1. 図1で、点Aと点Bは接点です。∠x の大きさを求めてください。数学Aの円で使う定理・性質の一覧 円周角の定理 弧ABに対する円周角の大きさはつねに一定であり、その角の大きさは、その弧に対する中心角の大きさの半分である。 ・∠ACB=∠ADB ・∠AOB=2∠ACB=2∠ADB また、次の図のよ
これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ
円の接線の性質 角度
円の接線の性質 角度-逆に、「直角三角形の各頂点を通る円は、斜辺(直角に対する辺)がその円の直径になる」というのも重要な性質です。 円周角の定理の逆 図のように 「点a、点b、点p、点qにおいて、∠apq=∠aqbなら、すべての点は1つの円周上にある」 といえます。 極限 数Ⅱ円の基本(円の方程式&円の接線)を完全マスター! 公式と証明を丁寧に解説します! 高校数学 数学ⅡB 数学 円に関する問題は、基礎問題から三角関数を絡めた応用問題まで出題されるため、多くの大学で問題が扱われています



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog
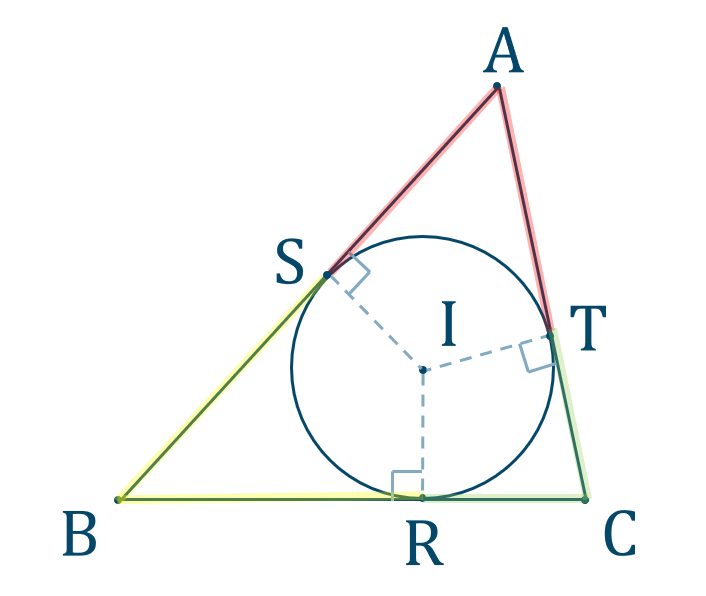
内接円といい、中心を内心といいます。 下の「定理8」は三角形の3つの角の二等分線は1点で交わること の証明ですが、その証明方法をはじめてみる方にとっては、「へぇ~ 垂線か」と思われるかもしれませんが、「角の二等分線」が「各辺から の距離 ここでは、接点を $(x_1,y_1)$ としましょう。これは円周上の点でもあるので\ x_1^2y_1^2=r^2 \が成り立ちます。 接線も接点を通ります。また、接線の傾きは、円の中心と接線を結んだ線と接線とが垂直に交わることから求めることができます。三角形の面積との関係 内接円と傍接円の半径は、三角形の面積に関係している。 S を三角形の面積、a, b, c を3辺の長さ、s を半周長としたとき、ヘロンの公式から、 = ( ) () () () = () 一方、内接円の半径は、 = () 辺 a に対する傍接円の半径は、 となる。 他の2辺に対する傍接円の半径は
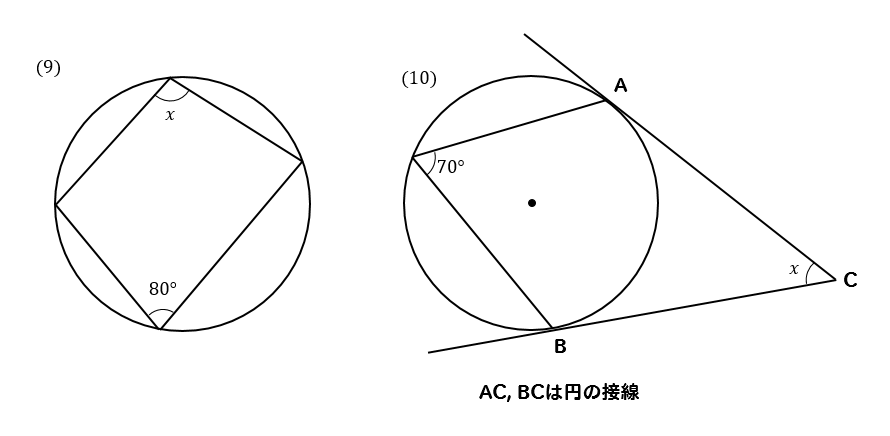
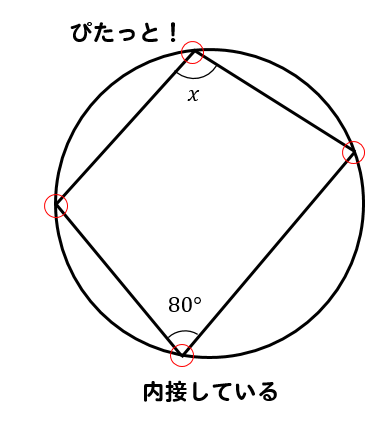
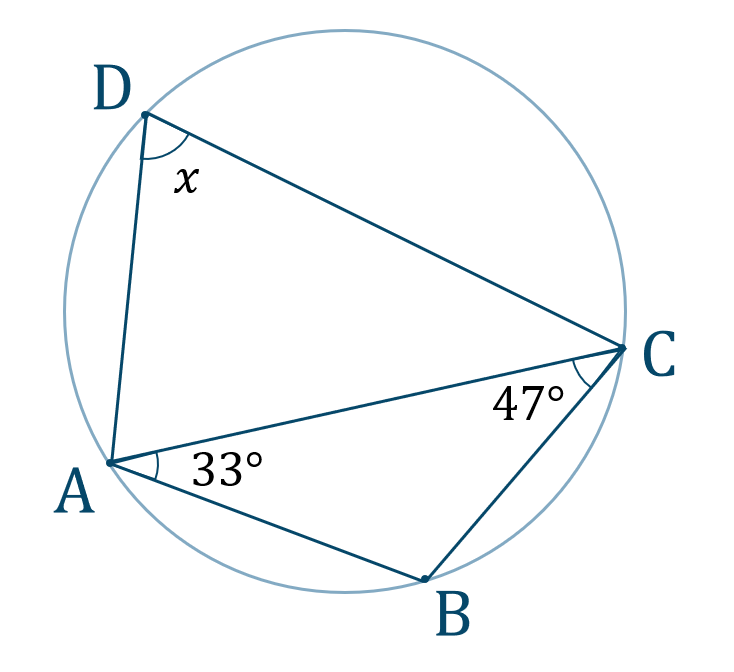
円に内接する四角形の角度 円に内接する四角形の対角の和は 180° である。 → a c = 180°, b d = 180° 円に内接する四角形の性質まとめ対角の和が180°になる理由 Tooda Yuuto 18年8月22日 / 19年9月9日 四角形の つの頂点 がすべて同じ円周上にある(内側から接している)とき、「四角形 は円に内接する」といいます。 反対に、四角形 の つの辺がすべて楕円の接線の方程式 楕円 x2 a2 y2 b2 =1 x 2 a 2 y 2 b 2 = 1 の周上の点P (x0,y0) ( x 0, y 0) における 接線の方程式 は, x0x a2 y0y b2 = 1 x 0 x a 2 y 0 y b 2 = 1 である.
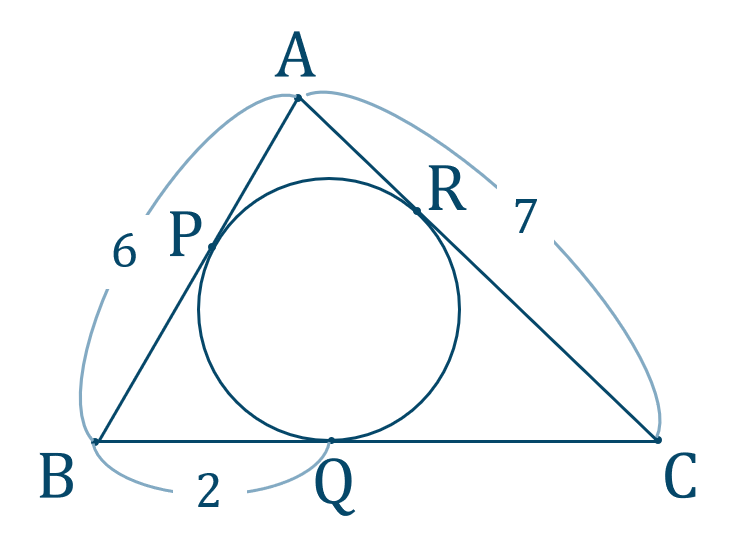
円 と 直 線 ①円の接線 円外の1点から円の接線をかく方法を考える。 接線の長さに関する問題を、三平方の定理や図形の 相似を利用して考える 2 ②円と相似 円と交わる直線でできる図形の性質を円周角の定理 と図形の相似を利用して考える。 2・円の接線の性質を確認する。 円の接線は ・作図方法を復習する。 円の接線の性質を板書する。 接点を通る半径に垂 直である。 ターレスの定理を復習し,板書す る。 3 課題についての説明を考える。 (30分) 課題 なぜ,このような方法で作図を行 えば 内接円の性質 内接円には、大きく \(2\) つの性質があります。 性質①内心と各辺の距離 多角形のそれぞれの辺が内接円の接線となっていて、各接点から引いた垂線の交点が内接円の中心(内心)となります。



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



知ってると得 円の接線の作図 円に接する円の作図方法 はてなラボ
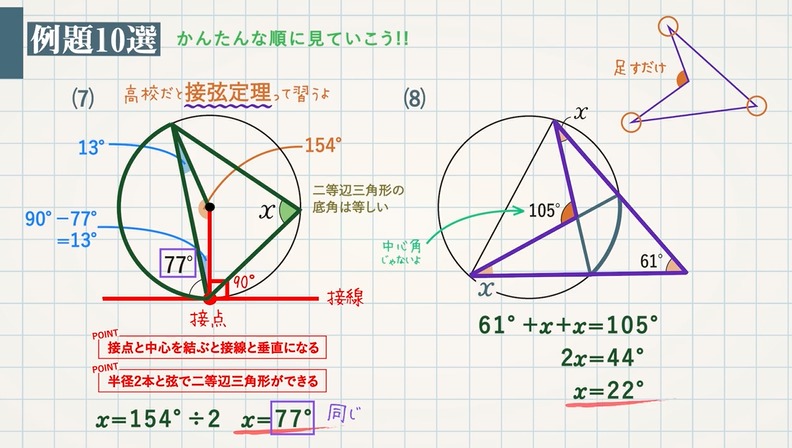
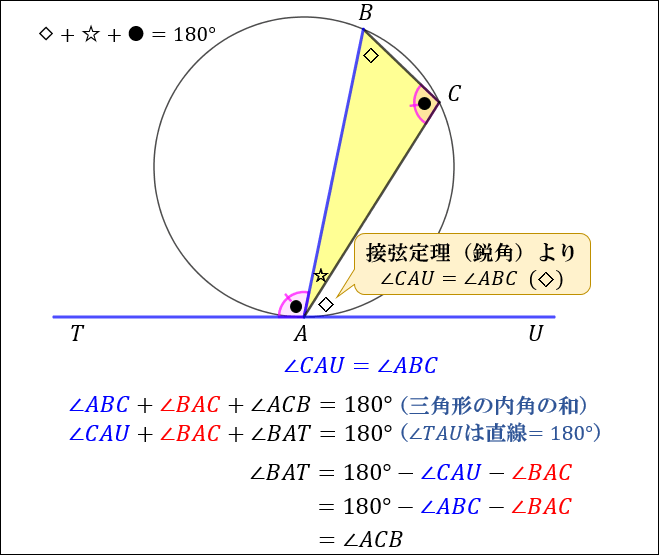
円周角の定理の極限 次に,接弦定理が成り立つことの感覚的な説明を紹介します。 点 c c c を円周上で限りなく a a a に近づけていくと, 円周角の定理より ∠ a c b \angle acb ∠ a cb は一定 直線 c a ca c a は円の接線に近づく 以上から接弦定理が成り立つことが納得できます。円と直線が同一平面状に存在するときには, ・ 2 点で交わる ・ 接する ・ 離れている の 3 つの場合が考えられます。 ここでは接するときを考えていきます。 円に接する直線のことを円の接線といいます。 また,このときただ 1 つの共有点のことを接点 といいます。 角度別に分かるその証明方法 18年8月9日 「円の接線 A T と弦 A B が作る角 ∠ B A T は、弦 A B に対する円周角 ∠ A C B と等しい」という定理を、 接弦定理 と言います。



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su



1
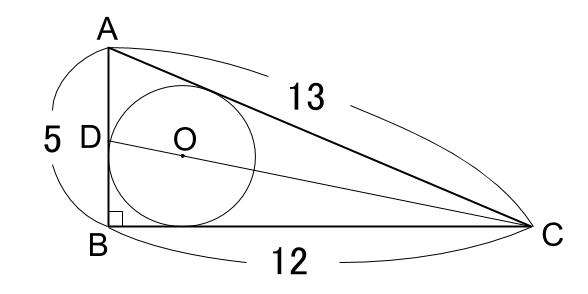
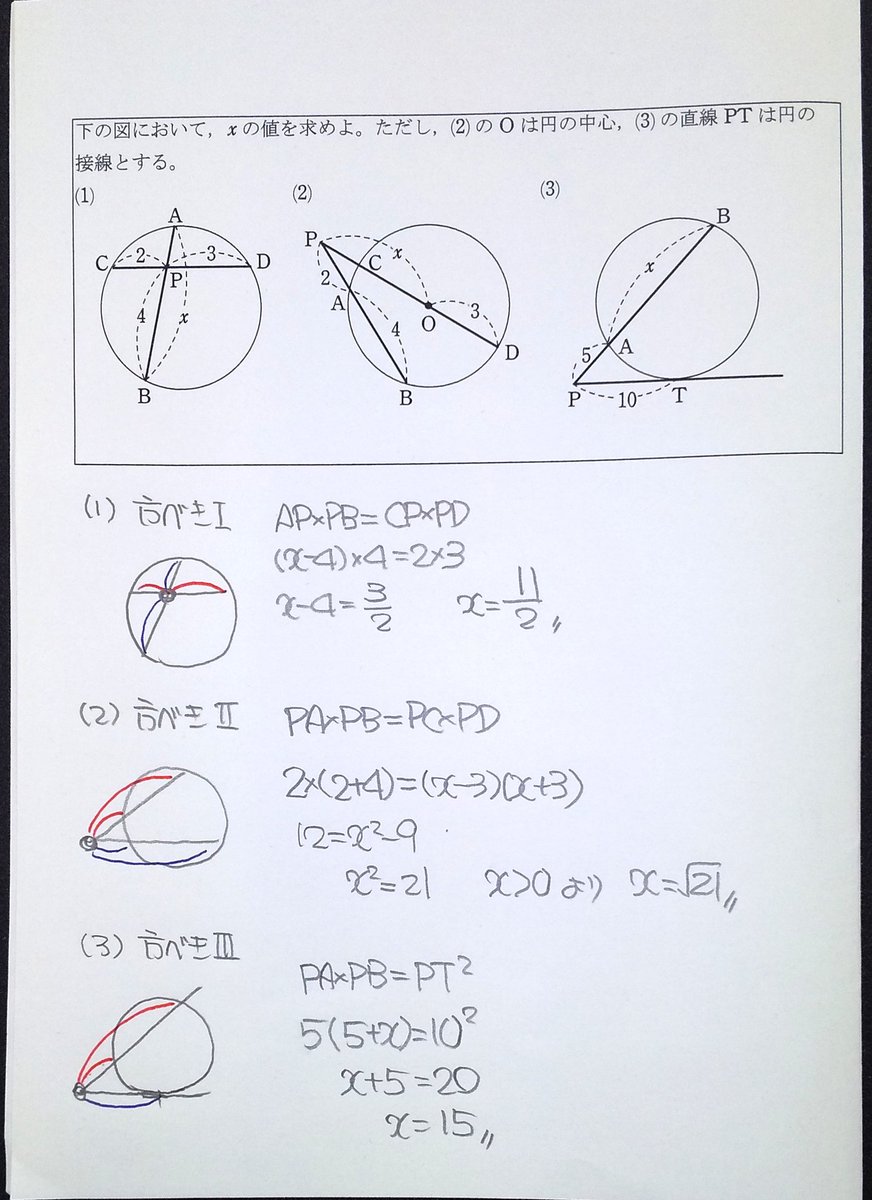
こんにちは。 da Vinch (@mathsouko_vinch)です。 接弦定理接弦定理は「円に内接する三角形とその円に接する接線があり、かつ三角形の"ある"頂点が接点となっている」場合に考えることができます。次のような状態の時ですね 高校数学Ⅱ 図形と方程式(円) 検索用コード 点 (7,\ 1)から円\ x^2y^2=25\ に引いた接線の方程式を求めよ$ \\ 円外の点から引いた接線の方程式}}}} \\\\ \textbf {「\textcolor {cyan} {点Aにおける接線}」ではなく,\ 「\textcolor {red} {点Aから引いた接線}」であるMathAquarium練習問題図形の性質 14 14 次の図において,x の値を求めよ。ただし,(3)の直線PT は接点をT とする円の接線である。 (1) (2) (3) Px A 9 D C 5 P B8 6 A D 4 C B x 3 2 P A T B x



内接円と角の2等分 中学数学の無料オンライン学習サイトchu Su




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
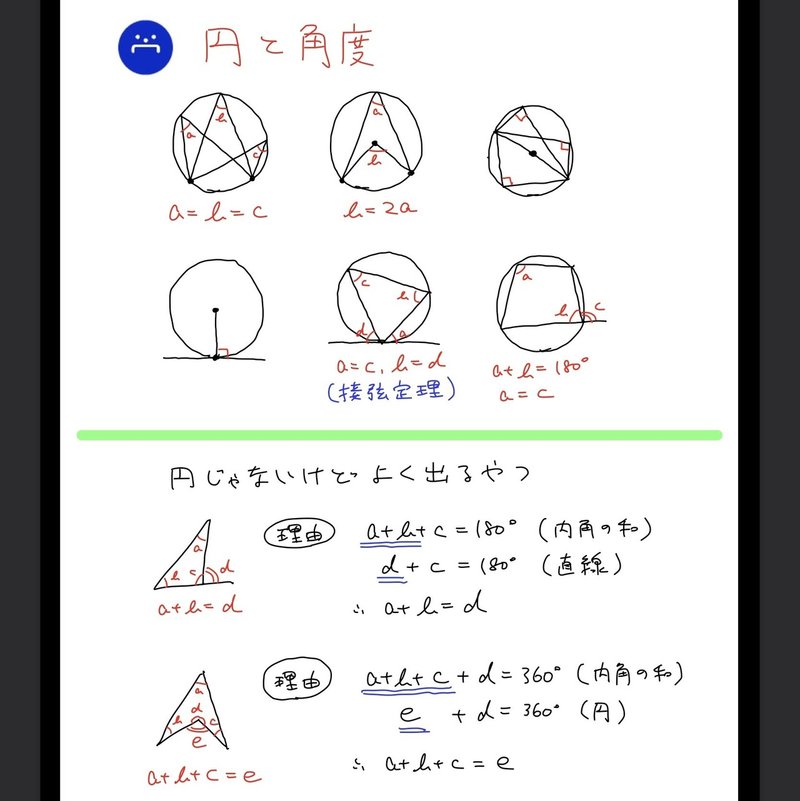
三角形の重心の性質 b 24 三角形の三中線は重心で交わり、重心は各中線 を2 1 に内分する ag∶gd=bg∶ge=cg∶gf=2∶1 21 円に内接する四角形の対角の和 a ab ch = 2 1 25 = 180° 22 円の共接線の長さ c ab=2√r×r 23 接弦定理aPtは3点 a , b , t を通る円の 点tでの接線 // 以上、円に関する性質でした! これらの「武器」と次の過程で学ぶ「三平方の定理」があれば 中学数学の円に関する問題で解けないものはないですね! お疲れ様でした! その他の問題は、「問題集」で !!円の性質 弦と弧 円周と2 点で交わる直線を割線という。 このときの交点を 2 点 a, b とするとき、円周によって、割線から切り取られる線分 ab のことを弦といい、弦 ab と呼ぶ。特に円の中心を通る割線を中心線という。中心線は円の対称軸であり、円の面積を 2 等分する。




高校数学a 共円条件 4点が同一円周上にある条件 受験の月



48s96ub7b0z5f Net En Sessen Fukusuu
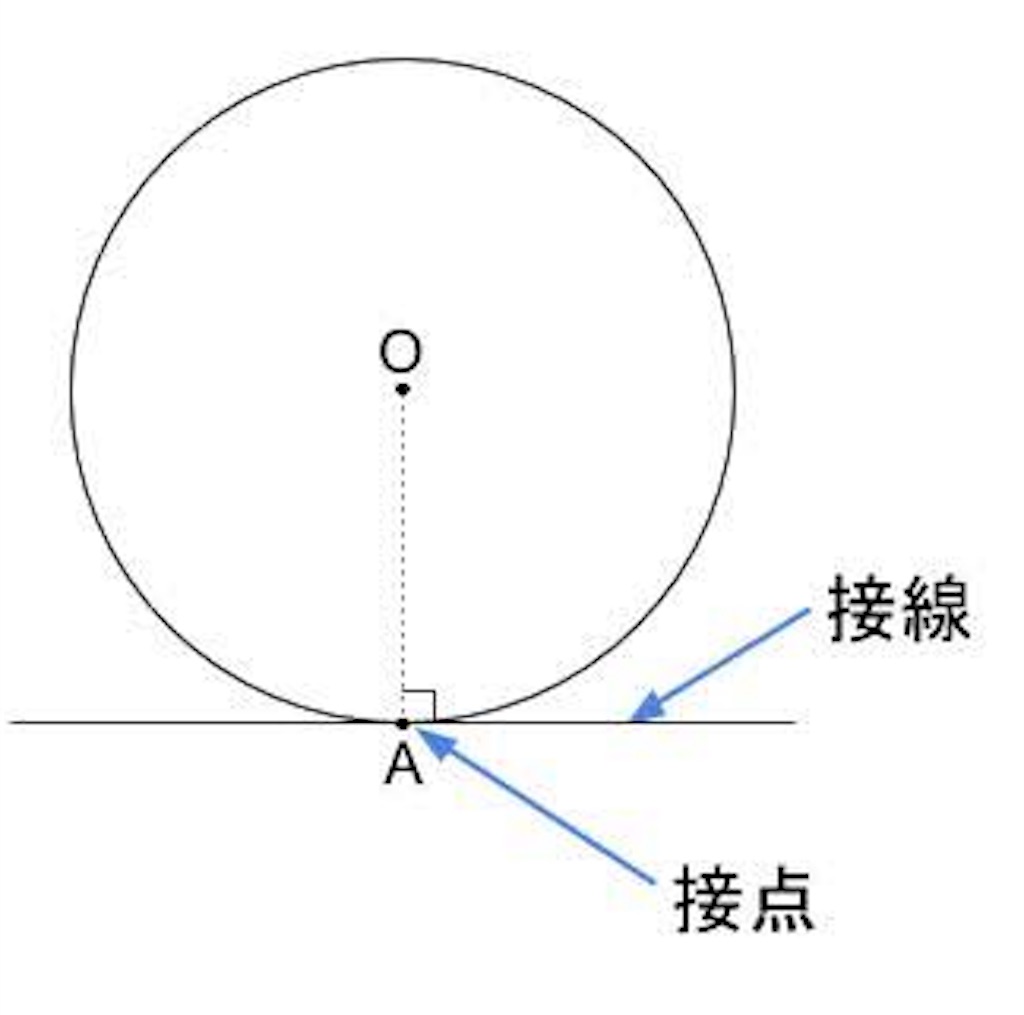
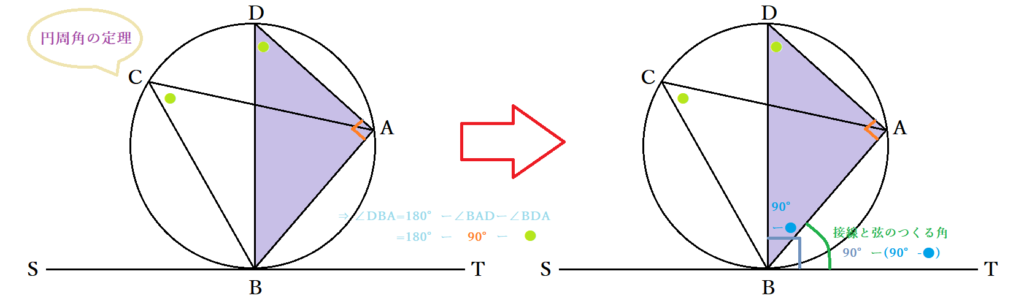
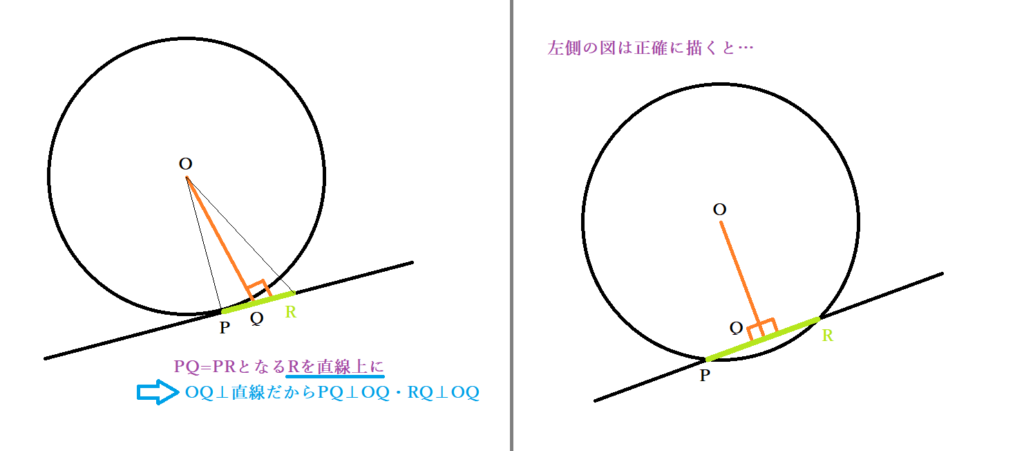
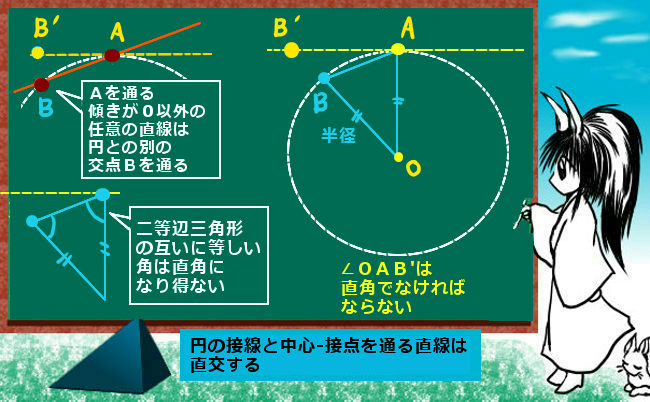
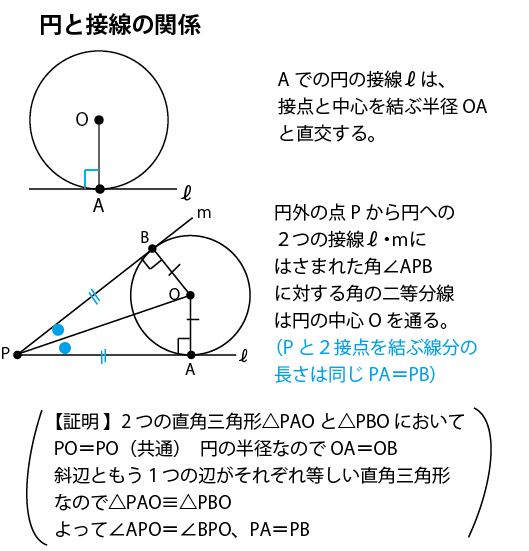
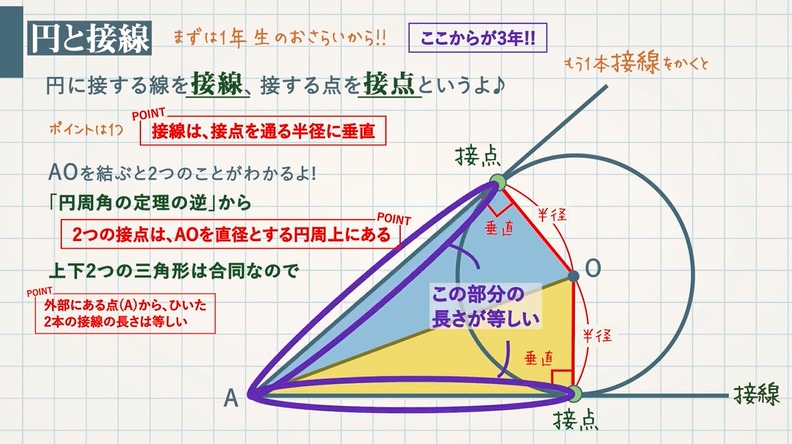
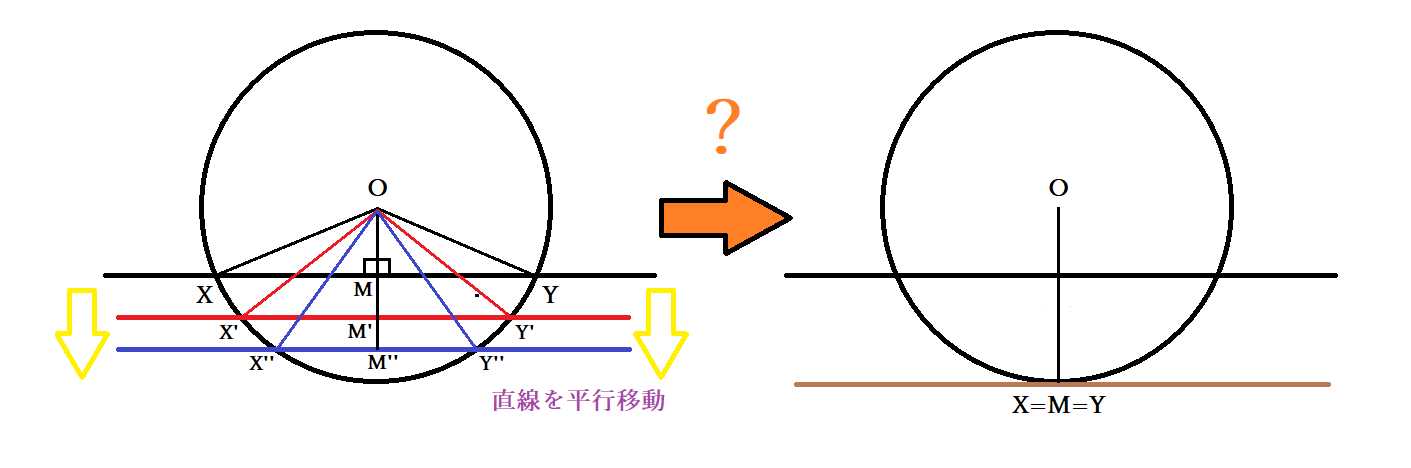
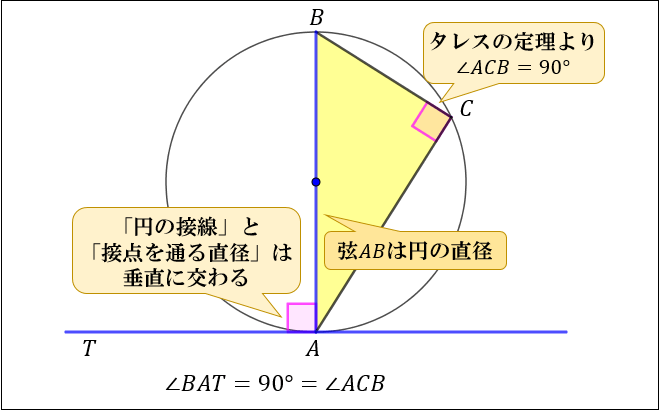
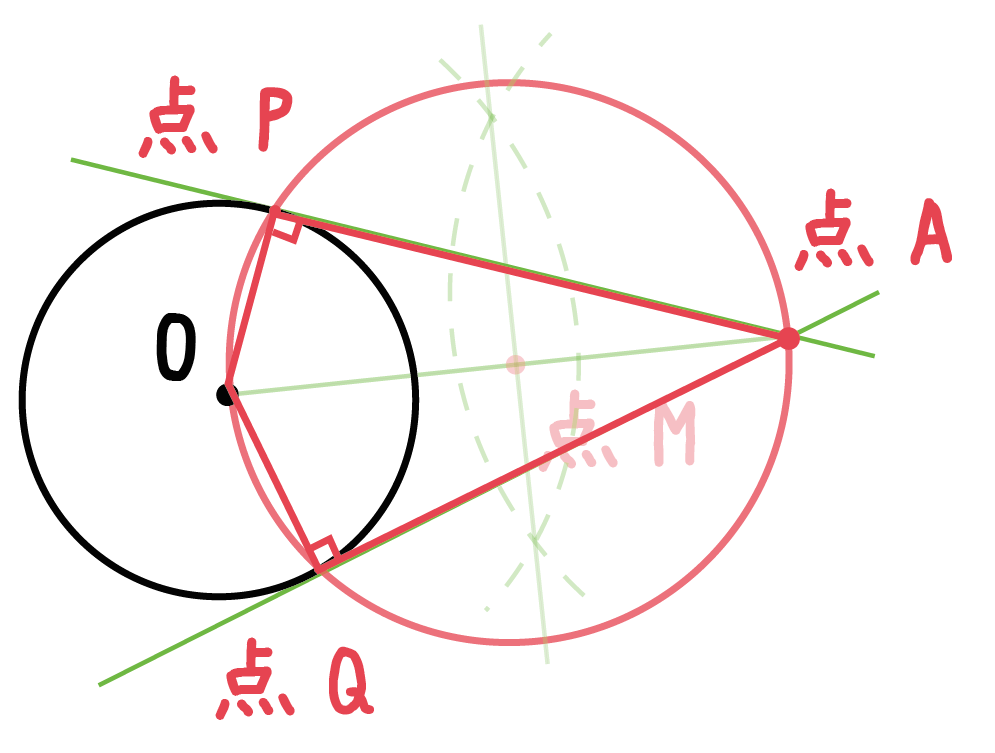
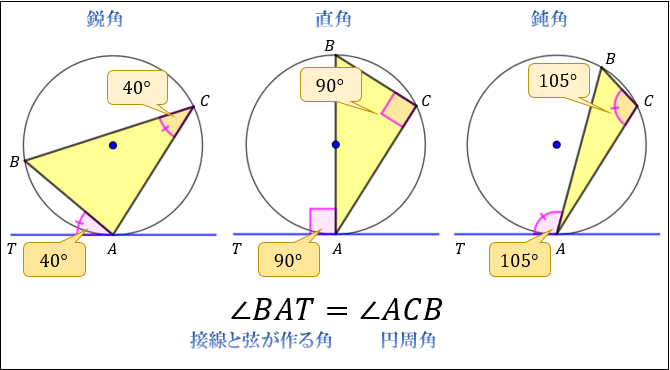
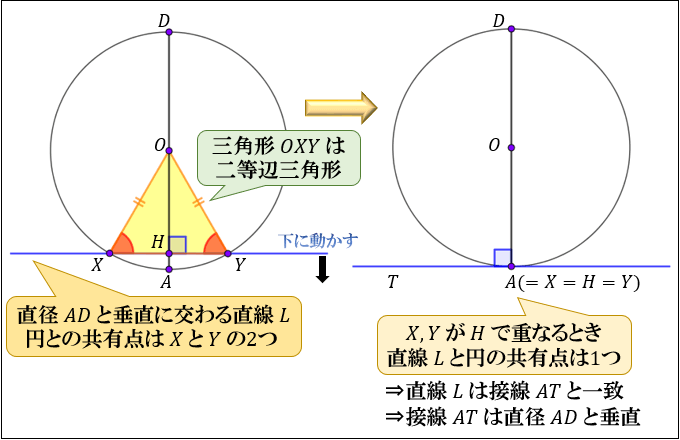
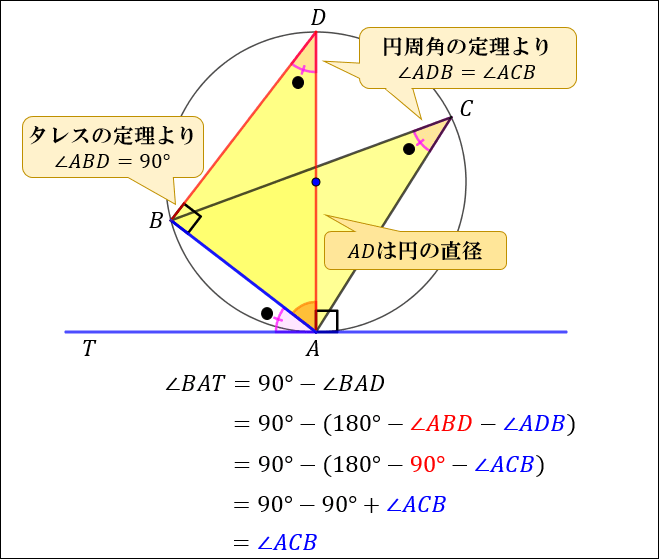
円の接線と弦の作る角が (1)直角 (90 ), (2)鋭角 (90 より小さい), (3)鈍角 (90 より大きい) の3つの場合に分けて示すこととします. (1) BAT=90 のとき (漢字2文字を入れなさい↓) 弦ABはになるので, (数字を入れなさい↓) BCA= ゆえに.BAT=BCAが成り立ちます円の接線 まずは1年生で学んだ円の接線について復習する。 直線が円とただ1点で出あうとき、この直線は円に接する(せっする)といい、この直線を円の 接線(せっせん) といい、出あう1点を 接点(せってん) という。「円の接線は、接点を通る半径に垂直」になる説明 まずは、下の図のように円と2点で交わる直線を引いて、円と直線の交点を点A、点Bとします。 円の中心を点O、 直線ABの中点を点M とします。 ここで、三角形AMOと三角形BMOは、3辺の長さが全て同じなので、合同な三角形になっています。




円に関する性質その1 接弦定理 高校数学の知識庫




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
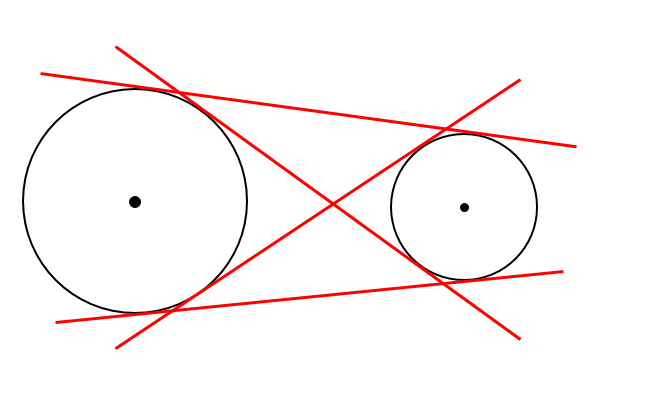
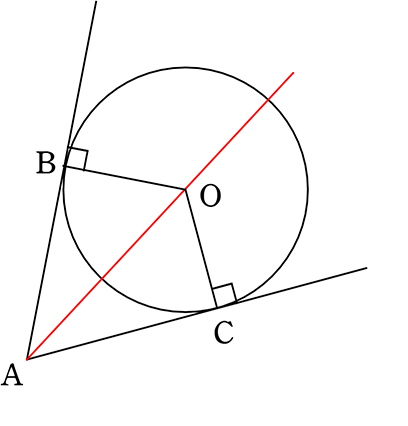
接線と円の関係についていろいろな関係があります。 ここでは、接線と円の関係である接弦定理などについて解説します。 接線の長さ かなり基本的な性質ですが、以下の様な定理が成り立ちます。 このように 「原点が中心の円」 で 「接点が ( x 1 − a, y 1 − b) である接線の方程式」 を考えることになります。 ここがミソです。 そうすると先ほど私たちが覚えた接線の公式が使えて ( x 1 − a) x ( y 1 − b) y = r 2 とできますね。 あとは 円を元の位置この接線を考える場合には、2円に次のような特徴があることを覚えておきましょう。 先ほどの接線の作図を理解できれば、こちらも同じような考え方で進めていきます。 まずはそれぞれの中心を通るような円をかきます。 その後、半径 となるような円




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
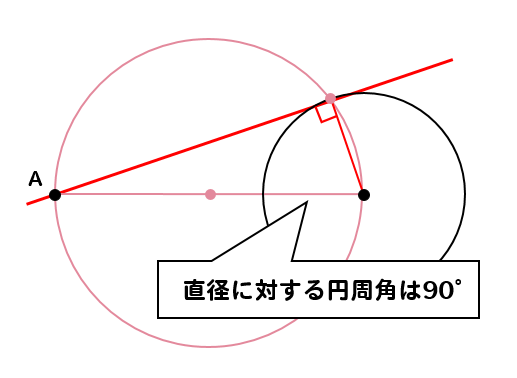
円の基本的な性質 弦、接線、接点という言葉は覚えていますか? その図形的性質は覚えていますか? 覚えていないとまったく問題が解けませんので、必ず暗記しましょう。 弦と二等辺三角形 円 \(o\) と外接円、外心について 「外接円」や「外心」の用語や意味は中学の 教科書の発展内容としてあります。 それぞれの各辺の垂直二等分線は一点でまじわり、その点Dを中心に円を書くと Dを中心に三角形の3つの頂点を通る円を書くことができて、この円図1のような円 o において,線分 ab は円 o の直径である。円 o の周上の点 c を通る接線と直線 ab との交点を d とする。 ∠ abc=25° のとき, ∠ bdc の大きさを求めよ。



公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学




接線と弦のつくる角の299 300までの解説をお願いします Clear
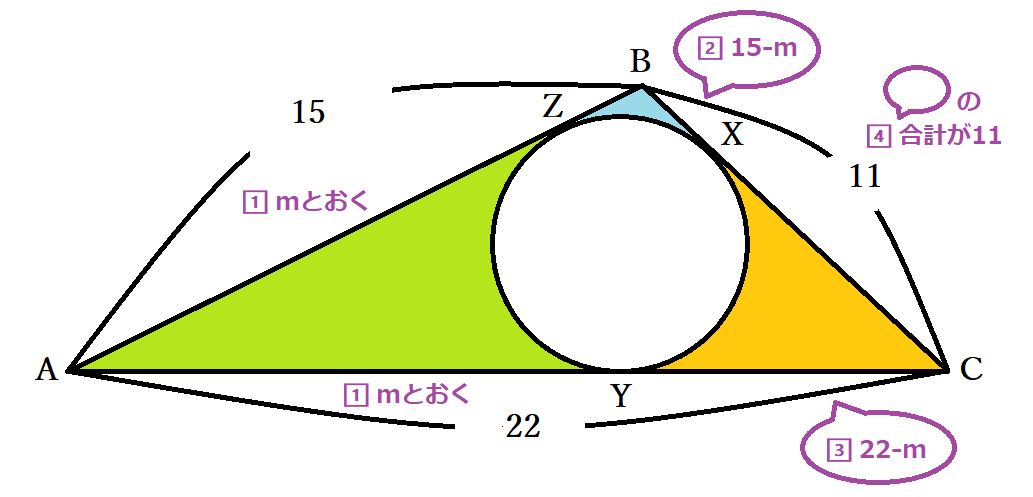
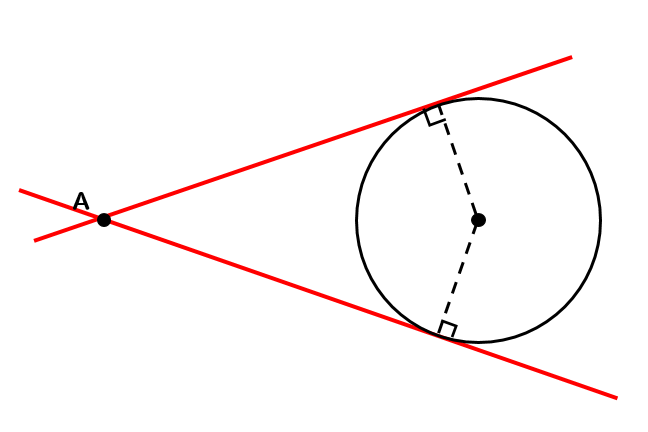
円の接線 高校受験などでよく出てきますね、 そこで円の接線の基本から作図、応用的な作図まで紹介します! 接線とは 接線の性質 円の外部の点を通る接線の作図 円の外部の点を通り円に外接する円の作図 (応用編)二つの円の共通接線の作図 (応用編)円の外部の二点を通り円に外接する円すれば、球外の一点から球に引いた2 つの接線の長さは等しいので、線分pf1とpf2の長さの和を考 えると pf1 pf2 = pp1 pp2 = p1 p2 =(球b1とb2の接する2円の間隔で一定) が示せる。 この性質を持つ図形が楕円と呼ばれる。 円と接線に関する3定理(垂直、接線の長さ、接弦定理) スポンサーリンク 高校数学A 平面図形 検索用コード 円の接線は,\ 接点を通る半径と垂直をなす 円の外部の点から引いた2本の接線の長さは等しい 接点を通る弦と接線が作る角は,\ その角



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ




数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog
「円周上の1点」と、 そいつと被らない円周上の2つの点を、 線分でむすんだときに、 できる角度のことを、 円周角(えんしゅうかく) とよんでいるんだ。 たとえば、つぎの円oがあったとしよう。 円周上の点をa・b・pとするよ。 このとき、 円の接線の方程式・公式 円の接線の方程式・公式は超重要なので必ず覚えましょう。 円の接線の方程式・公式(X-A)2 (Y-B)2 = R2 上の点 (X1, Y1)の円の接線の方程式・公式 ⇒ (X1-A) (X-A) (Y1-B) (Y-B)=R2 ※特に、中心が (0, 0)の円の方程式 ⇒ X1X Y1Y = R2 2



中学数学 円周角 中心角



Math 高校入試の難問 円と接線 働きアリ The 2nd



接弦定理とは 接線と弦の作る角の定理の証明 覚え方と応用問題 中学 高校 Curlpingの幸せblog



円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの幸せblog



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
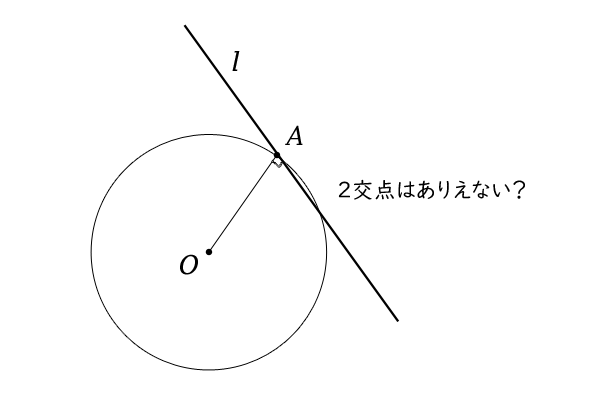



円と直線の距離と位置関係 特に交点 接点 接線について 高校数学マスター




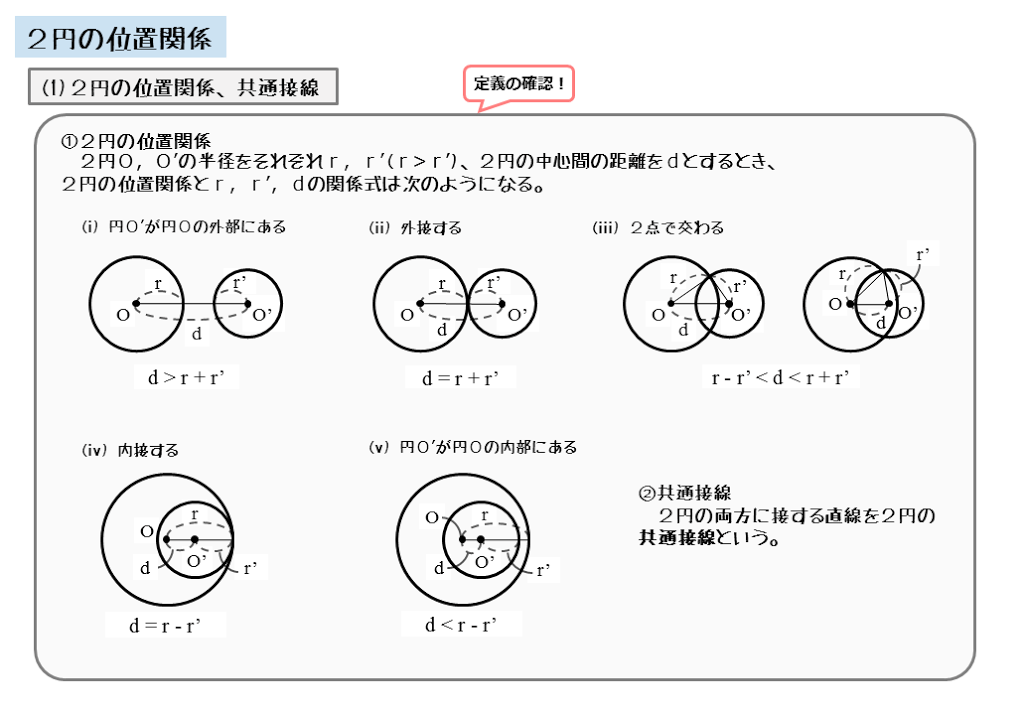
2つの円の位置関係と共通接線の求め方 図形と方程式 2
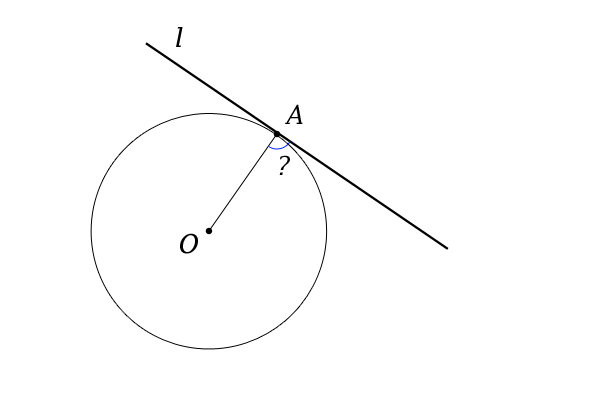



円と直線の距離と位置関係 特に交点 接点 接線について 高校数学マスター




接線と円の関係 Jsciencer
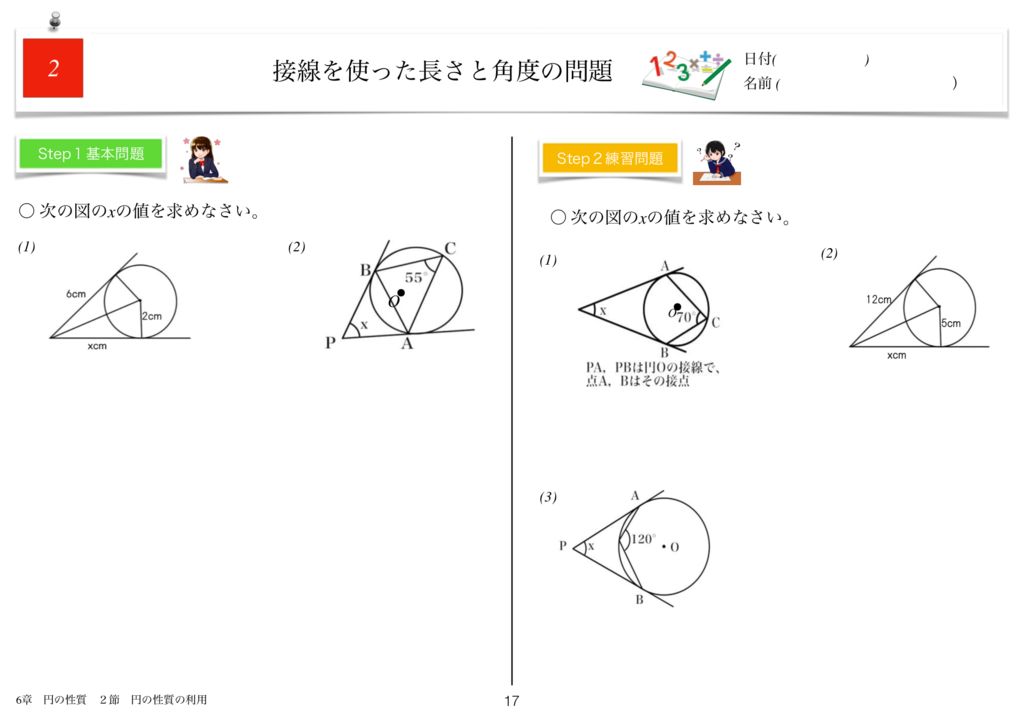



世界一わかりやすい数学問題集中3 6章 円の性質



円の接線と角度 中学から数学だいすき




接線の性質 なぜこの記号同士が同じ角度になるのかが分かりません Clear




円の接線に関する定理 公式 数a範囲 数学の偏差値を上げて合格を目指す




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



1
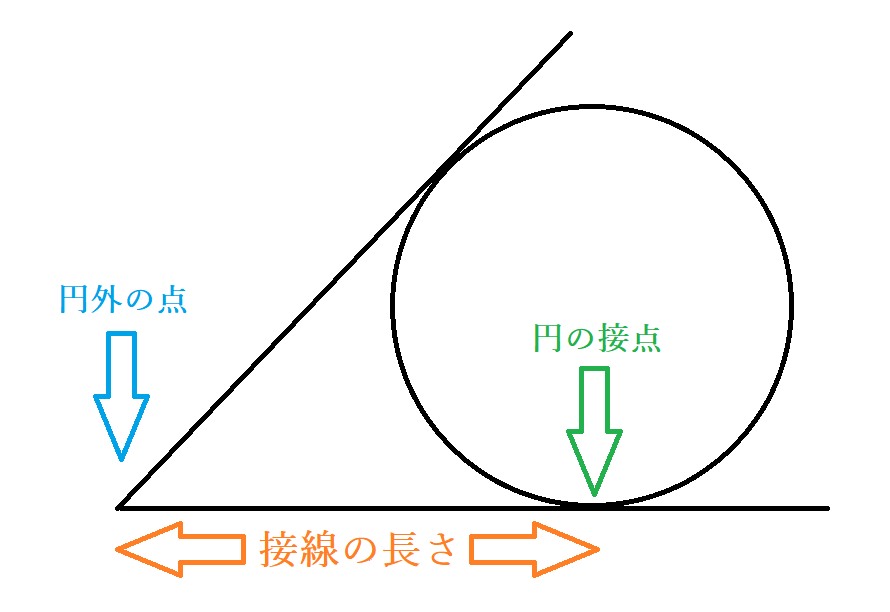



円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの幸せblog
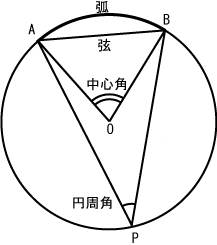



円 数学 Wikipedia




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
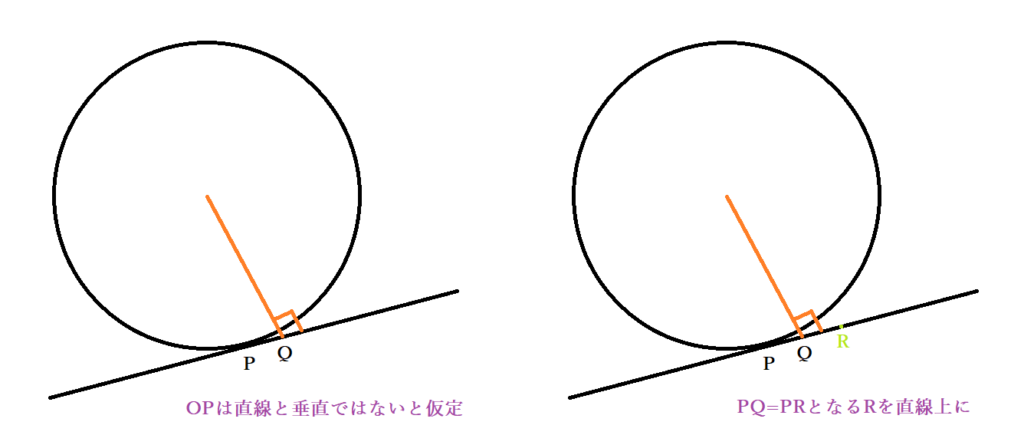



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog



atは円の接線である 角xを求めよ 写真の問題の解き方 Yahoo 知恵袋




接線と円の関係 Jsciencer




勉強しよう数学0 11



円の接線と内接 外接 理数系無料オンライン学習 Kori




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア
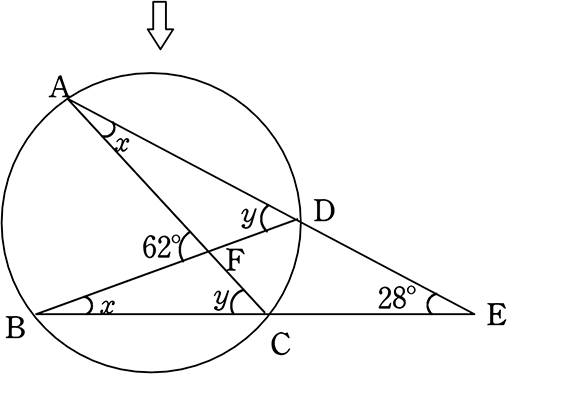



中学数学 円周角 中心角




接線と円の関係 Jsciencer




高校数学a 円周角と中心角のおさらい 例題編 映像授業のtry It トライイット




接線と弦のつくる角の定理 問題の解き方 証明をサクッと解説 数スタ



Math 高校入試の難問 円と接線 働きアリ The 2nd
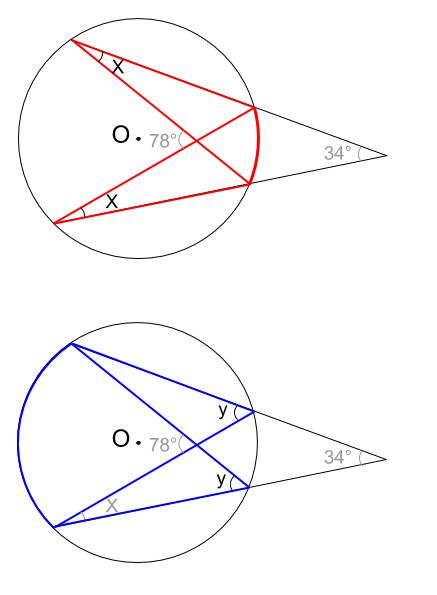



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su



1
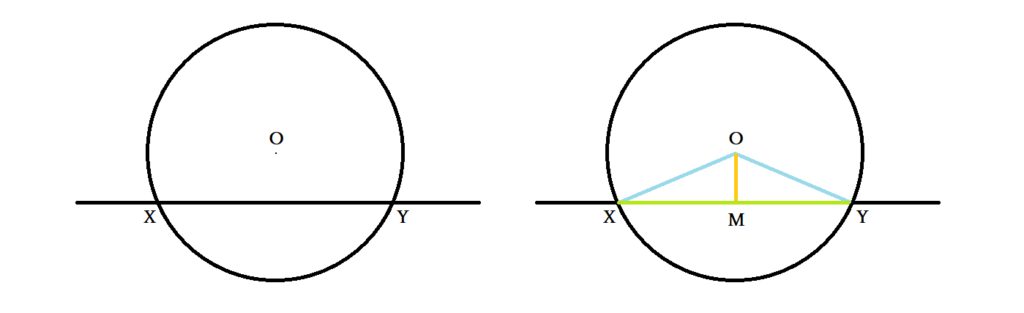



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog
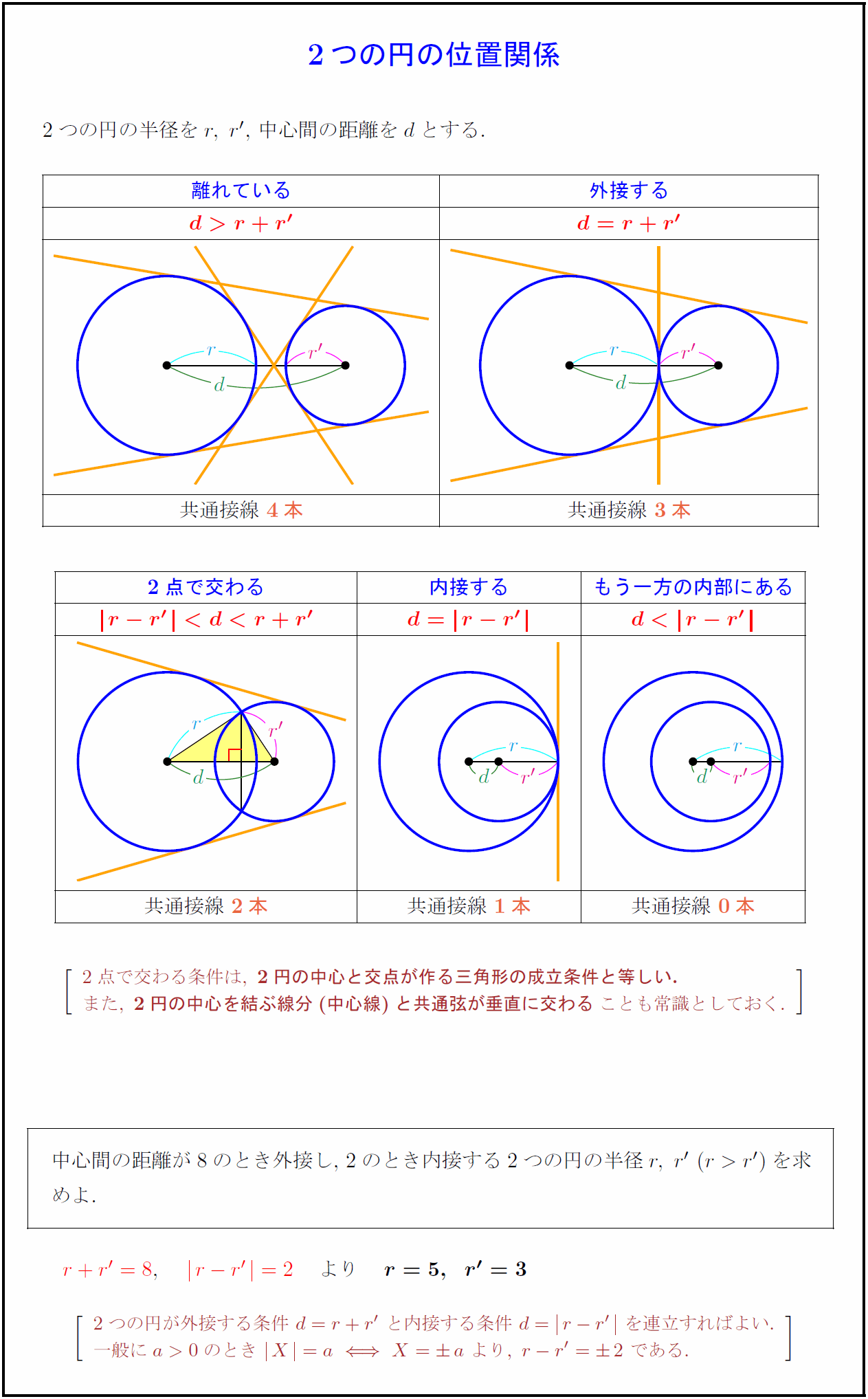



高校数学a 2つの円の位置関係5パターン 受験の月
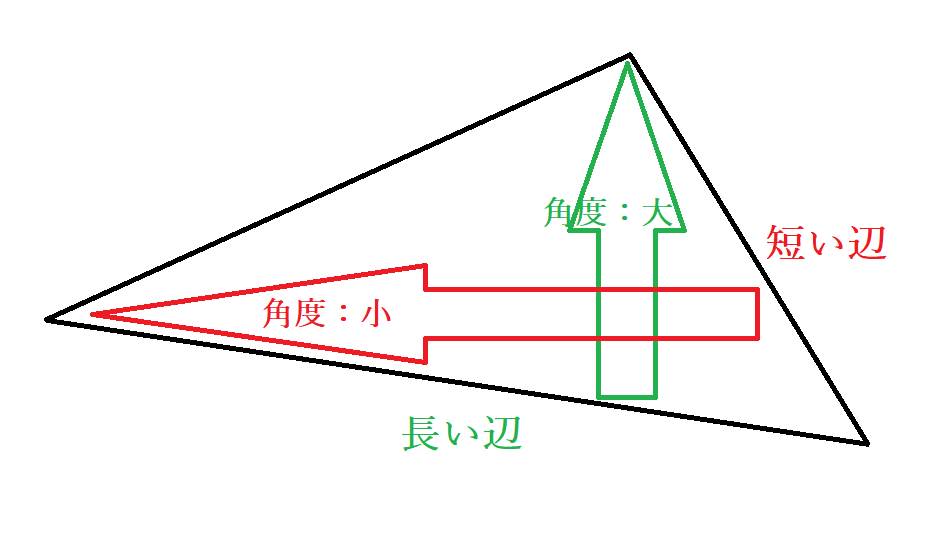



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog




高校数学a 2つの円の共通外接線と共通内接線の長さ 受験の月
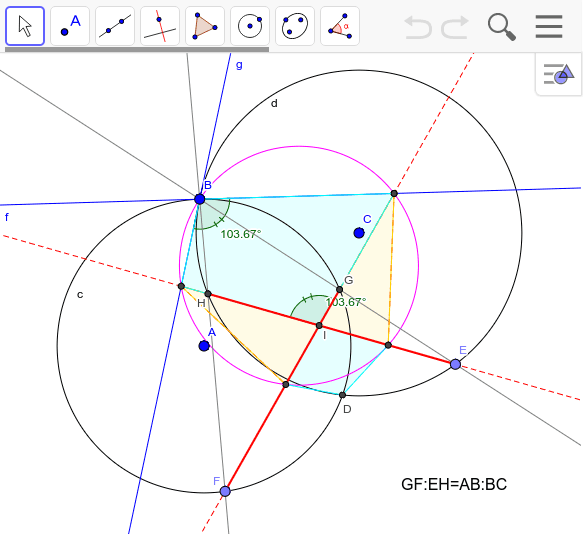



交わる二つの円に関する性質 Geogebra




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学



円と接線の性質を利用して図形の角度を求める問題 バカでもわかる 中学数学




円 接線 角度 円 接線 角度 中学 Trangjpsip




この問題で Bの角度とxの角度が同じになるのはなぜですか 教えてください Clear
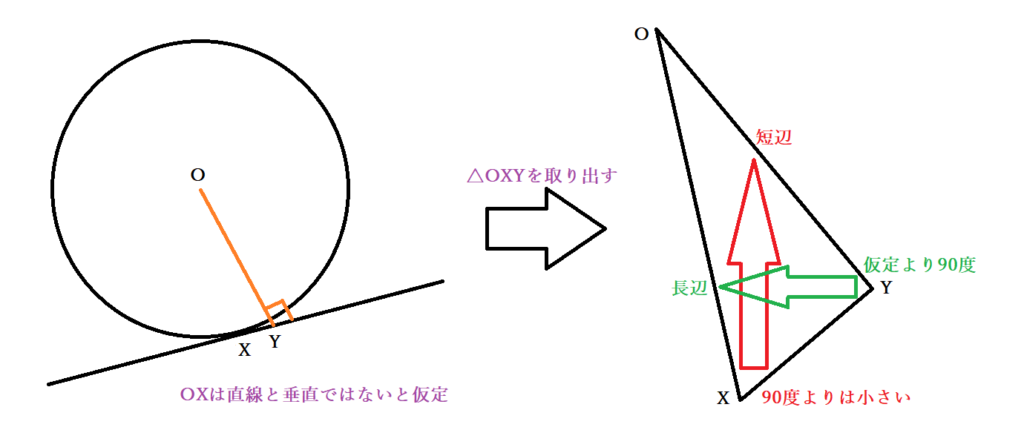



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ




円と接線 教遊者




円と接線の性質を利用して図形の角度を求める問題 バカでもわかる 中学数学



図形の性質 2円の位置関係について 日々是鍛錬 ひびこれたんれん
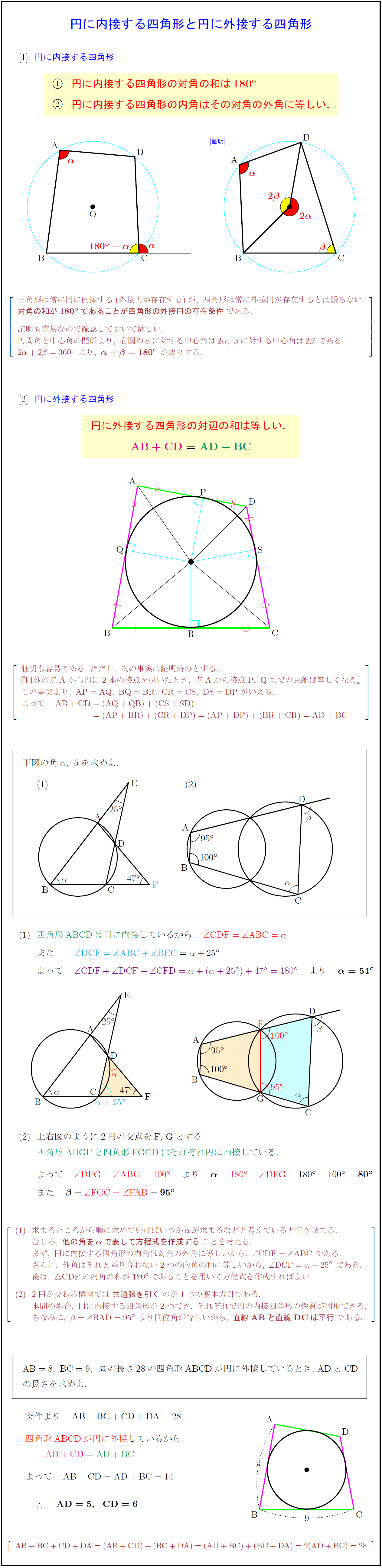



高校数学a 円に内接する四角形と円に外接する四角形の性質の証明 受験の月



図形の性質 Twitter Search



高校数学無料問題集 数a 第2章 図形の性質 円に関する問題 桝 ます Note



教科書レベルの問題一覧と解答 数学a 図形の性質 教科書より詳しい高校数学



17年前期 千葉県公立高校入試数学 第2問 5 作図 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



円と接線 教遊者



接弦定理




接線と弦の作る角 接弦定理 無料で使える中学学習プリント




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット



Math 高校入試の難問 円と接線 働きアリ The 2nd




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




円の中に三角形角度の求め方 いろんな角度の三角関數を単位円で考える Qmog Fi




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog




中学数学 円と接線 Youtube



教科書レベルの問題一覧と解答 数学a 図形の性質 教科書より詳しい高校数学



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ




円に関する性質その1 接弦定理 高校数学の知識庫



円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの幸せblog



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



中学数学 円の接線をサクッと作図する2つの方法 Qikeru 学びを楽しくわかりやすく



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ
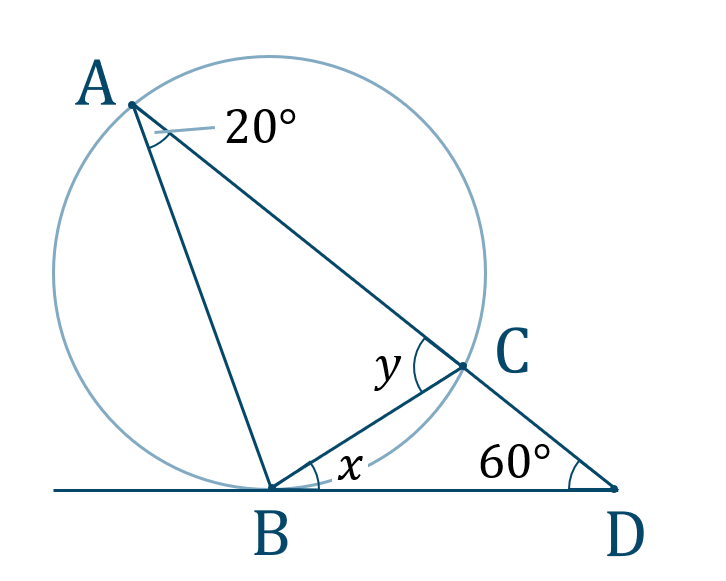



数学a 接弦定理の使い方とコツ 教科書より詳しい高校数学
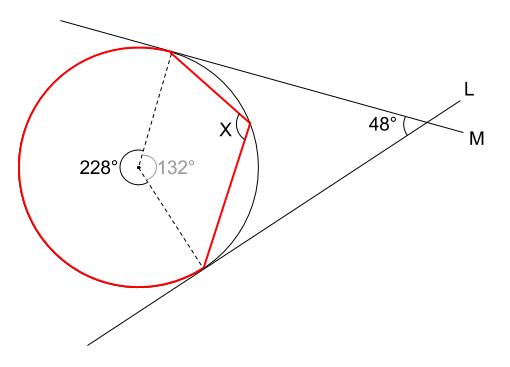



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su




円に関する性質その1 接弦定理 高校数学の知識庫
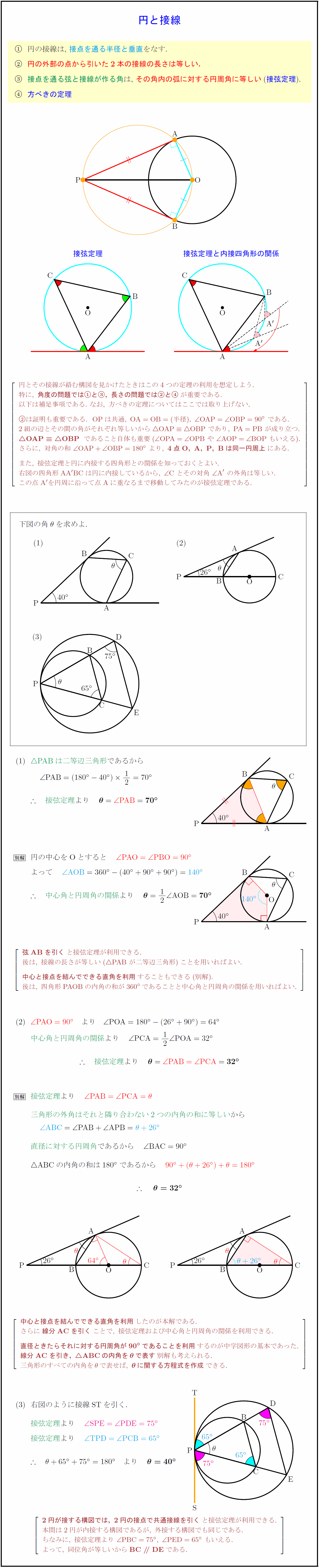



高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月
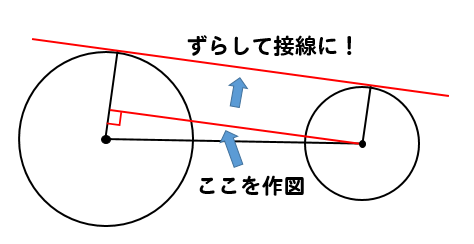



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ
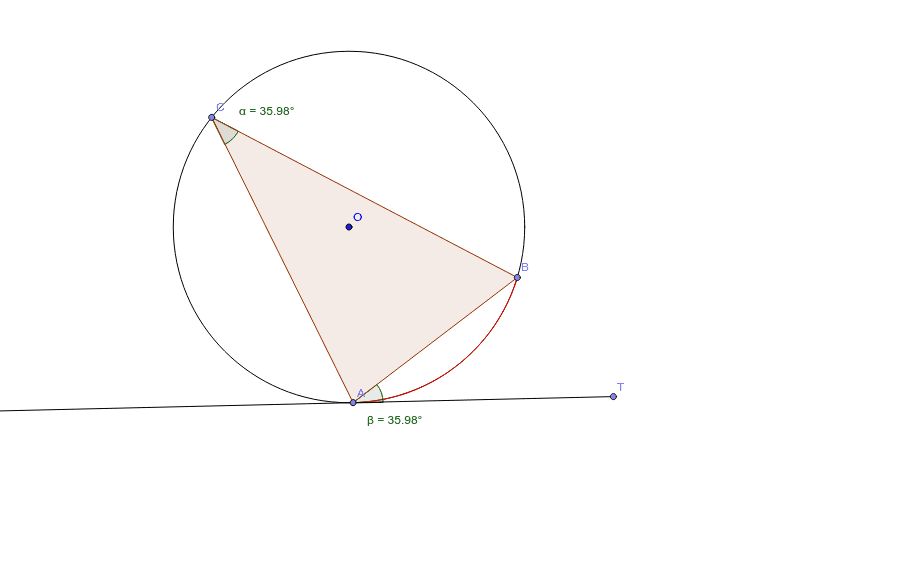



接線と弦の作る角 Geogebra



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ




これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



1




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア



中学校数学1年 円の接線の作図 Youtube
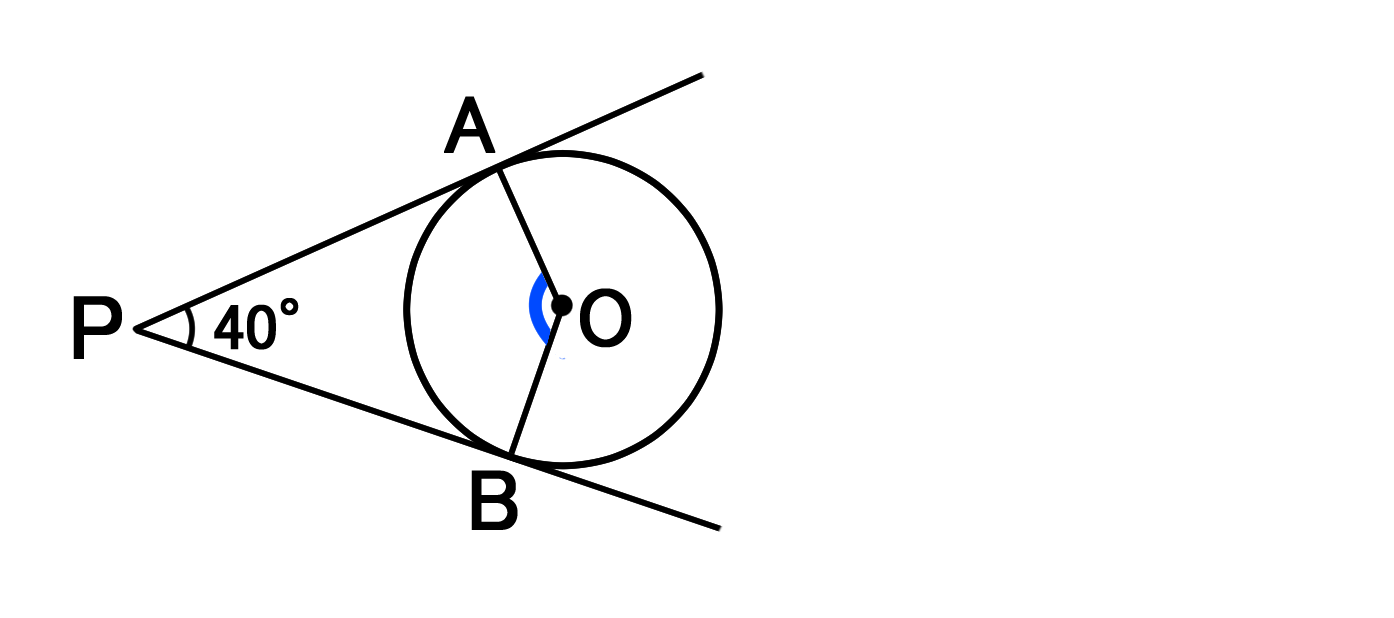



円と接線の性質を利用して図形の角度を求める問題 バカでもわかる 中学数学




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



中学数学 円周角 中心角
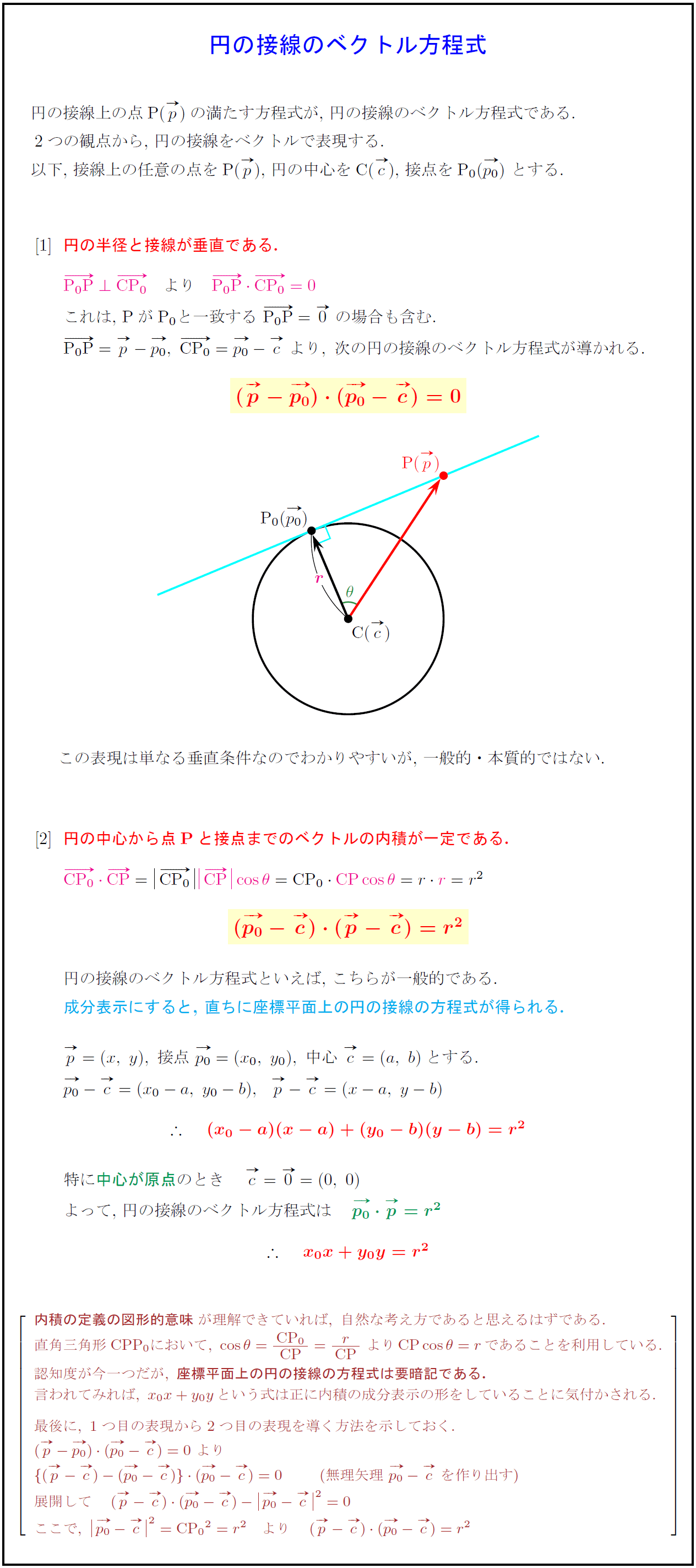



高校数学b 円の接線のベクトル方程式2パターン 受験の月



教科書レベルの問題一覧と解答 数学a 図形の性質 教科書より詳しい高校数学



0 件のコメント:
コメントを投稿